Structure et dynamique des erreurs conceptuelles
Un article de Caverne des 1001 nuits.
Version du 8 décembre 2007 à 10:28
Dans cet article, nous nous intéresserons à la création de concepts en tant qu'elle est une activité cérébrale majeure de l'esprit humain[1]. Nous pouvons aussi intégrer sous cette terminologie de « création de concepts » l'action de conceptualiser, donc d'une certaine façon d'abstraire depuis une situation particulière afin de tirer des conséquences pour une situation plus générale.
La conceptualisation, comme nous le verrons dans la suite de cet article, est à la fois une fonction vitale pour la psyché humaine, dans la mesure où elle est puissante et est à la base du raisonnement, mais elle est aussi le lieu des plus grands dangers du raisonnement au travers de ces merveilleux et périlleux outils que sont les concepts. Par certains moyens que nous expliciterons, ce danger peut se révéler d'une redoutable efficacité pour manipuler les masses et les foules, voire se manipuler soi-même avec des raisonnements dont la logique n'est pas à remettre en cause.
Sommaire |
Proposition d'analyse structurale des classes de concepts
Les types de concepts
Nous introduirons trois types de concepts suivant leur niveau de précision sémantique. Bien entendu, une démarche logique plus poussée nous obligerait à définir ce que peut être cette « précision » du contexte, voire à la quantifier. Bien que nombre de recherches dans ce domaine se passent de cet avertissement formel, nous tenons à le signaler dans la mesure où il est essentiel dans cette démarche de soulever les écueils qu'il nous faudra un jour résoudre et sur lesquels il faudra revenir. Néanmoins, il n'est pas dans l'objet de cet article de s'intéresser aux détails de cette qualification.
Nous distinguerons trois types de concepts :
- les concepts définis sans ambiguïté, dits concepts définis,
- les concepts flous, c'est-à-dire ceux qui peuvent proposer plusieurs sens et/ou plusieurs interprétations du ou des sens, ce genre de concepts étant nommés ambigus[2],
- les concepts qui représentent des choses qui n'existent pas, que nous nommerons concepts indéfinis.
Nous pouvons prendre des exemples de concepts des trois catégories. Par exemple, le concept “arbre” sera dit concept défini. Certes, ce n'est qu'un concept sous lequel se rangent à la fois d'autres concepts qui sont les classes d'arbres (“chêne”, “frêne”, “sapin”, etc.), mais aussi les instances singulières d'arbres (comme “le plus grand arbre de mon jardin”).
Comme exemple du concept ambigu, nous donnerons le concept de “liberté”. Ce concept trouve tout son sens dans un cheminement sémantique particulier. Il est souvent précisé par le contexte et par sa restriction à des situations précises (“la liberté d'expression”, “la liberté de circuler”, etc.). En ce sens, le concept de “liberté” est ambigu car il ne revêt pas toujours le même sens dans tous ses contextes d'utilisation. De plus, il offre un certain danger lorsqu'il est utilisé seul et sans précision. On parlera alors de “la liberté”, en général, sans trop savoir véritablement de quoi on parle.
Les concepts qui représentent des choses qui n'existent pas
L'avantage de cette classification de concepts est de proposer cette classe de concepts qui représentent des choses qui n'existent pas. Le but est de pouvoir refuser l'irruption d'un concept dans la mesure où ce dernier ne s'appuie sur aucun objet du monde connu, que ce monde soit matériel ou intellectuel.
Cette optique est tout à fait polémique, car les concepts sont toujours développés par des personnes ayant foi dans leur existence. Pour nous, en revanche, la foi dans l'existence d'un concept ne suffit pas pour que ce concept existe. Il faut démontrer que ce concept recouvre quelque chose plutôt que rien, ou nous pouvons alors échafauder n'importe quel raisonnement (juste ou faux) à partir d'un concept vide de sens.
Cette classe de concepts est donc, en quelque sorte, la « quarantaine » des concepts, l'endroit où on les place en attendant d'avoir statué sur leur compte. Le fait même de « mettre des concepts en quarantaine » est très révélateur d'un engagement critique envers les bâtisseurs de ces concepts, d'une méfiance pouvant être pilotée par l'incompréhension personnelle du sens du concept, ou le doute que ce concept ait véritablement un sens, dans l'absolu.
Cette dernière classe de concepts ne doit néanmoins pas être vue ou même être utilisée comme un outil servant commodément à refuser de discuter les concepts ségrégués. Au contraire, ces concepts entrent dans l'espace de la discussion, et comme nous le verrons, dans l'espace de la discussion souvent philosophique et parfois métaphysique ou théologique.
Il faut cependant isoler ces concepts de part le fait que leur structure est totalement différente de celle des autres concepts. Ils peuvent pour revêtir du sens impliquer des actes de foi, donc l'acceptation d'une axiomatique logique, qui, si elle n'est pas répréhensible, fait état d'un fonctionnement du concept logiquement tout à fait différent de celui des autres concepts. Ainsi, un arbre est un arbre, cela ne pose de problème à personne. Mais parler de l'“infini” est beaucoup plus mystérieux. Qu'est-ce que l'“infini” ? Ce concept existe-t-il dans la nature, dans notre univers où le nombre de particules est probablement inférieur à 10100 ? Les mathématiciens différencient souvent l'infini dénombrable et l'infini non dénombrable, ces différences ont-elles un sens ? Peut-on généraliser des résultats obtenus sur des ensembles de cardinal fini à des ensembles de cardinal infini parce qu'intuitivement, ce “passage à l'infini” nous paraît “normal” ?
L'“infini” sera donc, en terme d'exemple, l'exemple pris pour illustrer cette classe de concepts qui a priori ne représente rien qui puisse être attaché à la réalité.
Existence de la classe des concepts indéfinis
Bien entendu, le fait de trouver un concept inclus dans cette classe ne nous permet pas formellement de dire que cette classe existe. Beaucoup de mathématiciens seraient probablement d'avis que le concept d'infini est parfaitement défini. Cela montre la relativité subjective de la construction de cette classe de concepts.
Pourtant, si son contenu peut être débattu, son existence offre bien des avantages dans la mesure où elle permet de poser un problème quant à la nature des concepts eux-mêmes. Epistémologiquement, cette classe est tout à fait intéressante, car elle contient les concepts à problème, et donc les concepts qui vont être étudiés plus tard.
Poursuivons avec l'infini et avec la théorie Cantorienne des transfinis. Dans cette théorie, le mathématicien allemand Cantor définit des nombres infinis qu'il nomme transfinis, avec pour but de les comparer entre eux, de les additionner et de les multiplier pour former des types d'infinis. Poincaré fait très justement remarquer à l'époque que ces définitions sont tout à fait contestables et qu'il appartient à chacun de les accepter ou des les refuser. Pour ce dernier, les nombres transfinis ne servent à rien. Bien des années après en deux phases, des mathématiciens démontreront que l'irruption des concepts transfinis dans les mathématiques ne servent à rien, que l'existence de ces derniers soit acceptée comme axiome ou refusée. Le transfini apparaît aux yeux de l'épistémologue comme un concept indéfini.
La philosophie elle-même est prompte à créer ce genre de concepts. Prenons le “Dasein”, concept développé par Martin Heidegger dans sa philosophie. Il est, je crois, légitime de se poser la question de l'existence d'un tel concept, même si cette remise en cause peut choquer. Car, s'il ne s'agit pas forcément de remettre en cause la constitution de l'étant et les mouvements de l'être sur lui-même et par rapport à ses potentialités d'être, le fait d'introduire un concept fondateur ontologique à ce niveau est tout à fait discutable. On peut alors se poser la question de savoir si les interrogations sur l'étant du Dasein ne sont pas construites de toutes pièces comme peuvent l'être les interrogations sur les transfinis de Cantor.
Force est de constater que l'on assiste dans la pensée humaine à une activité de création de concepts indéfinis structurelle qui, si elle est loin d'être néfaste notamment parce qu'elle a très souvent le mérite de changer la perspective d'analyse des problèmes complexes, n'a de sens que dans une démarche épistémologique de tri dans ces concepts[3]. Insistons sur ce point très important. Le progrès conceptuel pourrait résider dans cette classe de concepts qui, une fois créés, seraient examinés pour devenir des concepts d'une autre classe (ou définis ou flous mais plus indéfinis). Par contre, si le concept séjourne trop longtemps dans la classe des concepts indéfinis, on peut dire qu'il y a un problème structurel de fond de décalage entre le fait que le concept survive dans les esprits alors qu'il reste indéfini.
Foi et concepts
Pour qu'un concept soit à la fois utilisé et qu'il reste indéfini, il est nécessaire que ce concept soit supporté par une foi, une croyance. Néanmoins, il est nécessaire de distinguer deux types de concepts indéfinis :
- les concepts à caractère religieux,
- les concepts à caractère non religieux.
Ainsi, le concept de “Dieu” est naturellement un concept de la classe des indéfinis, mais il est très différent a priori du concept de “Dasein” dans la mesure où il est de notoriété publique que ce concept a un sens si celui qui l'utilise a la foi. Les concepts à caractère religieux sont donc à la fois indéfinis mais ne peuvent exister qu'au travers de la foi. On comprend donc tous les conflits d'interprétation théologiques dans la mesure où cette non définition du concept encourage les lectures personnelles et donc divergentes, les interprétations du concept. Néanmoins, la foi implique un cadre d'axiomes logiques permettant d'utiliser ces concepts indéfinis à caractère religieux (par exemple “Dieu existe et est omnipotent, omniscient, éternel”, etc.). On pourra donc logiquement et structurellement être méfiant quant à l'usage des concepts religieux indéfinis.
Les concepts indéfinis à caractère non religieux sont, eux, beaucoup plus pernicieux car, contrairement aux concepts religieux, ils présupposent une foi non consciente. Pour utiliser des concepts indéfinis comme si ces derniers l'étaient, il faut accorder une foi à celui qui les a développé ou à ceux qui les enseignent. Il est donc important de noter que, structurellement, l'utilisation de concepts indéfinis repose aussi sur des axiomes, repose aussi sur des principes (souvent moraux ou sociaux ou même religieux). En d'autres termes, le concept non religieux à caractère indéfini masque une véritable croyance et très souvent une représentation inconsciente du monde donnée a priori.
C'est pourquoi il est souvent très facile de critiquer les raisonnements religieux avec des concepts indéfinis, car si le combat prend des airs intellectuels, il ne s'agit toujours que d'une reformulation d'un débat autour d'une foi (par exemple foi en la laïcité contre foi religieuse). En d'autres termes, les concepts indéfinis dans leur plus grande latitude sont des concepts dont l'utilisation requiert une foi certaine, religieuse ou pas.
Typologie structurelle de l'erreur
Cette classification simpliste des concepts exhibe une typologie structurelle de l'erreur, tout d'abord dans les concepts flous, mais aussi et surtout dans les concepts indéfinis. Ces derniers renvoient à une représentation collective du monde, que cette collectivité soit nationale, ou plus limitée (congrégation religieuse par exemple). Les concepts indéfinis font donc toujours référence à une branche de l'inconscient collectif, dans lequel on retrouve des principes moraux notamment, des échelles de qualité, de confiance et des classifications sociales établies.
Proposition d'analyse dynamique de la création de concepts
De la conceptualisation
La conceptualisation est le processus selon lequel divers éléments singuliers peuvent être placés sous la même entité ou sous la même dénomination. Structurellement, la création de concepts est donc une approximation dans la mesure où elle gomme les spécificités des objets singuliers qu'elle inclut sous la même idée et ou sous la même terminologie.
La conceptualisation est une nécessité de la pensée humaine qui, immergée dans des phénomènes divers et variés dont beaucoup se ressemblent, a besoin de sortir de cette série de phénomènes afin d'en tirer des concepts qui à leur tour évolueront au fil de l'expérience. Conceptualiser est donc à la fois une nécessité et une approximation[4]. En ce sens, la conceptualisation est le mécanisme de base de la représentation.
La conceptualisation est souvent vu comme une généralisation, comme une globalisation d'un ensemble de phénomènes ou d'objets pouvant obéir aux mêmes lois ou à la même désignation terminologique. Là encore, en utilisant les mots de la phrase précédente, nous sommes dans le concept, et donc dans l'approximation, lorsque nous constatons qu'il n'est pas aisé de donner une définition exhaustive de la conceptualisation. Derrière cette difficulté, apparaît l'aspect « dimensionnel » du concept, c'est-à-dire l'ensemble des interprétations non forcément totalement corrélées qui pourraient recouvrir sa sémantique complète dans tous les contextes de son utilisation. C'est cette remarque qui nous a poussé a établir la classification simple proposée dans la première partie de cet article.
Dimensions et conceptualisation
La conceptualisation, en tant qu'elle est connue et pratiquée, a souvent pour effet non seulement de gommer la cardinalité des phénomènes ou objets qu'elle représente, mais aussi de supprimer certaines « dimensions » des objets qu'elle « généralise ». Mais qu'appelons-nous au juste dimension d'un phénomène ou d'un objet ?
La dimension d'un mot ou d'un phénomène pourrait être représentée par, respectivement, les différents sens de ce mots ou les différentes manières de percevoir ce phénomène. La conceptualisation unit en opérant souvent une « agrégation unidimensionnelle » le long de la dimension qui semble la plus importante dans le contexte utilisé. En un sens, la conceptualisation pourrait être vue comme une projection d'un phénomène ou d'un mot sur une "droite" arbitraire (mono-dimensionnelle). Cette projection agirait, en ce sens, comme un opérateur de diminution de la complexité des objets étudiés.
Nous sommes là devant un problème métaphysique, puisque :
- d'une part, le mécanisme de conceptualisation est supposé généraliser,
- d'autre part, l'action qui vise à gommer les différences entre les objets permettant la création d'un concept est une action de simplification.
Or la généralisation et la simplification ne sont pas des concepts totalement identiques :
- un des sens attachés à la généralisation est le sens logique du "pour tout objet de tel type",
- un des sens attachés à la simplification est le sens logique du "tel objet est environ égal à".
La volonté de proposer un autre vocabulaire (celui des dimensions et des projections) pour aborder la conceptualisation met en exergue un sens adjacent à la notion de généralisation : celui de la simplification.
Vers un modèle de la conceptualisation
Nous allons tenter de poursuivre plus loin la construction de ce modèle de conceptualisation. Dans le cas de l'approche projective que nous venons d'évoquer, les phénomènes ou les mots regroupés sous le même concept auraient la même image sur cette droite, qu'ils soient issus d'une conceptualisation par généralisation (et donc soient relativement homogènes au moins dans une de leurs dimensions) ou par projection d'entités différentes (il s'agit là d'une proposition et non d'une démonstration).
Penser reviendrait, dans ce modèle, à trouver la dimension de réflexion ad hoc afin d'y projeter les concepts eux-mêmes sur cette "droite" et d'opérer à des comparaisons des résultats par usage de « mesures » de type classique : plus grand que, plus important que, plus petit que, négligeable par rapport à, égal, comparable ou identique. La pensée devient acte de projection dans un espace mesurable.
L'analogie à laquelle nous nous référons est bien entendu une analogie géométrique. Plus précisément encore, comme nous allons le voir par la suite, nous userons d'une analogie topologique.
La complexité des concepts
L'ébauche de modèle exposé ci-dessus met en lumière des concepts simples issus de la projection d'objets multidimensionnels sur une espace monodimensionnel, soit une "droite" (nous utiliserons une image euclidienne). Nous pourrions généraliser ce modèle en considérant les hypothèses suivantes :
- il est très difficile de distinguer ce qui est phénomène pur du mot qui le désigne et même qui le présente à notre conscience (ce qui lève le problème de la perception de la singularité que nous ne traiterons pas ici),
- le concept a lui-même plusieurs dimensions et s'il est le résultat d'une projection d'un ensemble d'objets sur une autre entité, le concept est souvent aussi un objet multidimensionnel, même si sa dimension est inférieure ou égale à la dimension des objets dont il est la projection.
Nous admettrons, pour le moment, concernant le premier point, que la perception de la singularité n'est pas « intellectualisable »[5]. La seconde hypothèse est, elle, plus facile à admettre intuitivement. Il résulte de ces deux hypothèses la reformulation suivante :
- A) tout est concept dans l'intellect (et non pas dans la psyché) ; le singulier est inaccessible à notre intellect (mais pas à notre sensibilité) ; cela revient à dire que tout est, intellectuellement parlant, représentation[6] ;
- B) tout concept est un objet multidimensionnel qui peut être projeté sur un espace de pensée de dimension finie, très souvent réduit à une dimension un ou deux, rarement trois et exceptionnellement plus, afin d'y être mesuré à d'autres concepts : ce mécanisme intervient dans la réflexion.
Tentative de formalisation basique du modèle
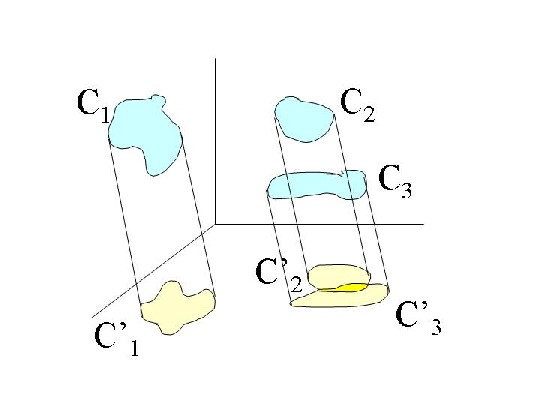
Le modèle que nous pouvons prendre est celui d'un espace vectoriel normé (l'introduction d'une norme est importante dans la mesure où les projections doivent être mesurables) de dimension n où chaque concept est défini par un point ainsi que par un voisinage pouvant se représenter mentalement comme une “boule” déformée. La projection de ce concept sur un hyperplan P de dimension k<n donne une “zone” de dimension k. Si plusieurs concepts ont sur l'hyperplan P une partie commune de leur projection, on peut définir sur P le concept résultant de l'intersection des projections des voisinages.
La figure 1 montre un exemple simple en trois dimensions où trois concepts C1, C2 et C3 sont projetés sur un plan P (dans l'exemple le plan z=0). Si on appelle p la projection, on voit que p(C1) ∩ p(C2) = ∅, mais que p(C2) ∩ p(C3) ≠ ∅. On peut donc contruire le concept résultant de l'abstraction de C1 et C2 à partir de cette intersection. D'où une proposition de modèle simplifié de conceptualisation.
Le second mouvement de la conceptualisation
L'objet résultant de la projection est un objet de dimension k dans un espace de dimension n. Dans une deuxième phase de la conceptualisation l'esprit humain aura tendance à généraliser cette projection à un nouveau concept de dimension n qui lui est illicite logiquement. Nous pourrions nommer cette généralisation une « complétude des dimensions ».
Pourquoi ce mouvement de complétion des dimensions ? Pour la simple raison que l'esprit manipulant des objets de dimension n, si la conceptualisation s'est faite par projection et a réduit la dimension de l'objet, l'esprit humain aura tendance à extrapoler sur l'objet simplifié (p(C2) ∩ p(C3) dans la figure 1), d'où une extrapolation qui peut, à la fois être à la source de questions fertiles, mais aussi à la source d'erreurs logiques fondamentales.
Bien entendu, il ne s'agit là que d'une ébauche très lointaine de modèle basé, qui plus est, sur des visions intuitives. Cependant, l'avantage de ce modèle est de proposer une lecture de l'erreur due au second mouvement de la conceptualisation.
Exemple
Nous pouvons aussi illustrer cette erreur de second niveau par l'exemple suivant, moins abstrait que ce qui vient d'être exposé, exemple qui parsème un grand nombre de raisonnements quotidiens.
Supposons que nous ayons construit le concept de "réalisateur de film" en prenant d'une certaine façon, la partie commune de réalisateurs non engagés politiquement. Nous avons, lors de la création de ce concept de réalisateur de film commis une simplification en oubliant que réalité était plus complexe que notre conceptualisation. Nous avons projeté sur un espace de dimension plus faible. Le concept même que nous avons construit est plus pauvre que l'ensemble des choses que nous pourrions dire sur l'ensemble des réalisateurs de films et pourtant ce concept s'impose à nous comme une généralité qui masque les particularités que nous ne voyons pas. La deuxième phase de généralisation nous a fait accepter l'idée que notre projection en dimension k était vraie en dimension n. Nous avons donc complété notre concept implicitement en lui donnant une légitimité conceptuelle totale. Nous avons extrapolé.
Supposons maintenant que nous ayons à critiquer un réalisateur A qui lui est engagé. Logiquement, nous serons en droit de dire : A n'est pas un réalisateur de films, car il est engagé. Le problème logique se situant derrière cette affirmation est la création du concept de réalisateur de film qui pour nous est composée uniquement de réalisateurs non engagés. On pourra constater que la morale n'est pas lointaine dans cet exercice. Nous avons biaisé la logique pour démontrer ce que nous voulions démontrer et non ce qui était a priori démontrable. La structure de l' a priori réside donc dans le fait que nous avions simplifié (projeté) plus généralisé cette simplification (complétion dimensionnelle) pour arriver à une conclusion logique qui n'est au final qu'une redite tautologique de nos hypothèses implicites de la projection que nous avons utilisée[7].
Cet exemple illustre que le mécanisme même de la conceptualisation est un mécanisme soumis à des erreurs par le fait qu'il soit impossible à notre esprit de manipuler des concepts incomplets (au niveau dimensionnel) et que nous soyons irrésistiblement entraînés à les généraliser à des choses qu'ils ne sont pas.
Conclusion
Aussi bien de manière structurelle que de manière dynamique, la conceptualisation ou l'utilisation de concepts est un processus qui est indispensable à la pensée humaine mais structurellement soumis à l'erreur. Cette erreur est donc indissociable des mécanismes de base de la pensée humaine. Il convient donc, comme nous l'aborderons dans un prochain article, de développer une véritable psychologie de l'erreur.
Catégories: Article | 1001nuits | Logique | Philosophie