Vers une topologie des concepts
Un article de Caverne des 1001 nuits.
Sommaire |
L'aspect multidimensionnel des concepts
- Formalisation : le concept est une boule à n dimensions (voisinage).
- Les concepts dépendent des langues => la notion de voisinage.
Formalisation des liens entre concepts
Introduction du deuxième type d'objets
Difficultés de formalisation
- Règles qui peuvent être topologiques, mais aussi discrètes
- La non identité du concept avec lui-même => introduction des plans de raisonnements, espaces de projection
- La projection des liens entre concepts
- Généralités sur la réduction dimensionnelle
Les lois d'échelles en concepts
- Les plans se projettent les uns sur les autres => simplification pour raisonnement ; parcours dans les liens d'inférence
- Le concept global n'est souvent connu que par la série de ses projections (phénomènes)
- Le concept est bâti par agrégation de projections différentes => généralisation dimensionnelle et perte de spécificité
- Un concept est composé d'autres concepts (discrets mais pouvant être vus comme des projections)
En cours
ℵ "est" un espace de Hilbert
- H espace engendré par P, base des nombres premiers (hormis 1).
- P est une famille orthonormale de H. P est libre.
- ∀ x dans H, ∃ (ki)i ∈ ℵ : x = ∏i ∈ ℵ piki.
De fait, ℵ est engendré par ∪i ∈ ℵPi (sous base avec les i premiers nombres premiers), alors que P engendre ℵ ∪ {∞} sachant que {∞} est insuffisant pour décrire les typologies de divergence des objets mathématiques générés par P et non éléments de ℵ.
ℵ est un espace "fractal dimensionnel" ?
Tout n de ℵ peut être associé à un vecteur de composantes sur P.
On définit la fonction f1 :
- f1 : ℵ → ℵ∞,
- n → (n1, ..., nM, 0, 0, ...) tels que n = ∏i ∈ ℵPini.
f1 est la première transformation.
Cas particulier. n a M composantes sur P, ni. Chaque ni a Mi composantes sur P. Cela exhibe le problème de définition entre composante et vecteur. Nous sommes dans un espace qui est spécial, car les "scalaires" sont aussi des vecteurs du même espace. Donc l'algèbre linéaire ne s'applique pas vraiment. Cela montre aussi le problème de la "nature" de l'opérateur.
Soit un espace E. On a ∃! (ni) : n → (ni). n est un "arbre".
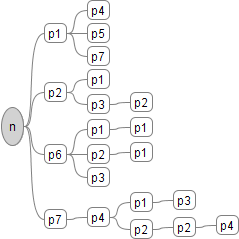
Exemple : n = 27.11.13 . 353.2 . 1322.32.5 . 17725.337, on peut représenter n de la façon suivante.
Soit P, la base des nombres premiers : p1 = 2, p2 = 3, p3 = 5, p4 = 7, p5 = 11, p6 = 13, p7 = 17, etc.
Formalisation
Soit C, l'espace des concepts. C est de dimension finie N.
Tout élément de C possède des "composantes" qui sont des "hyperformes".
Soit P, l'ensemble des espaces inclus dans C tels que dim(P) < N. On notera Pk, un élément de P de dimension k. Tout concept de C peut se projeter sur Pk.
Soit :
- c1 ∈ C ;
- c1 :